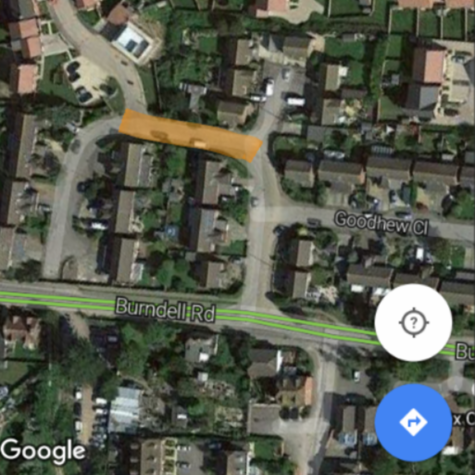
Improved Access to Emerald Gardens/Navigation Drive

 Maxine K. signed
just now
Maxine K. signed
just now  Adam B. signed
just now
Adam B. signed
just now 
The access to the c. 170 houses on the Emerald Gardens Development, Yapton is via Goodhew Close and is inadequate. The key stretch of the access as highlighted in the attached picture is the reason for this petition. It is constantly parked on, both sides, making the access restricted and dangerous.
All those who have signed this petition support the application for a Traffic Regulation Order (TRO) to have yellow lines painted on the stretch of road (both sides) highlighted in the attached photograph.
The basis for the application is categorised below in accordance with TRO guidelines:
1. Safety
- the parking of vehicles in this stretch of Goodhew Close given the high volume of traffic, relative to the accessibility of the site, represents a hazard to road users as either end is immediately preceded/followed by blind corners. Thus users are forced on to the wrong side of the road without being able to see what is coming.
- this is an area heavily populated by families and small children, many of whom use the footpaths by the highlighted road. Any increased hazard on the road increases risk to pedestrian injury.
2. Traffic Conditions
- Emerald Gardens is inadequately serviced in respect of access to and from the main road. A development of this size should not be dependent on such limited access via another narrow preceeding estate. Whilst this is unlikely to be capable of remedy, everything that can be done to ease the situation should be done. Yellow lines on the highlighted stretch would significantly ease the situation.
3. Economy and Environment
- This application has a neutral impact on the economy and environment.
4. How People will benefit
- currently only three people (with off street parking) feel the need to park on the road in such a fashion that causes problems for over two hundred people. If one applies the Utilitarian maxim, greatest good for the greatest number, the the benefit calculation is easy.



Enter your details on the next page
Comment
See More 0